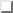Reißfestigkeit

Die Reißfestigkeit  (technisch: Höchstzugkraft  bzw. Höchstzugspannung)  einer Faser ist bestimmt durch die maximale Spannung, die durch eine axial an der Faser angreifende Kraft  erzeugt wird. Diese Spannung bewirkt eine Verformung der Faser, mit der eine Querschnittsverringerung  einhergeht. Der Zusammenhang zwischen Kraft und Verformung wird in Kraft-Dehnungs-Diagrammen  für das jeweilige Material wiedergegeben.

Steigert man die Zugbeanspruchung  kontinuierlich, wird zu einem stoffspezifischen Zeitpunkt die Höchstzugkraft-Dehnung der Faserprobe  überschritten und sie bricht. Bei der Beschreibung von Faserfestigkeiten  steht im allgemeinen die Höchstzugspannung im Vordergrund. Da diese bei der Anwendung  im textilen Bereich meistens nicht einmal annähernd erreicht wird, benutzt man immer häufiger die Dehnung  als Vergleichsgröße (s. Verspinnbarkeit). Besonders interessant ist dabei das Dehnungsverhalten unterhalb der Höchstkraft-Dehnung bei Berücksichtigung der Einwirkdauer.  Es beschreibt die elastischen und plastischen Eigenschaften   der Faser sowie deren dynamisch-mechanisches Verhalten. Letzteres ist bei den im Gebrauch oft vorkommenden Wechselbeanspruchungen   besonders wichtig.

In der Tabelle sind sowohl für Baumwolle  als auch für Hanf  verschiedene, aus der Literatur entnommene, werkstoffkundliche Werte  aufgeführt.

 
Tabelle:   Stoffwerte für Baumwolle und Hanf. Quelle: [28, 10], eigene Umrechnungen

Es sind darin sowohl feinheits- sowie querschnittsbezogene Höchstzugkräfte bzw. -spannungen als auch die zugehörigen Höchstzugkraftdehnungen angegeben. Diese Werte weichen erheblich von der theoretischen Festigkeit  ab, die vom gleichmäßigen Tragen aller Hauptvalenzbindungen  innerhalb der Faser ausgeht. Für Zellulose   ergäbe sich dabei eine theoretische Festigkeit von 8000 N/mm [10]. In der Praxis sind aber die Hauptvalenzen nicht für die Festigkeit entscheidend. Vielmehr werden bei Zugbeanspruchung  die Kräfte über Nebenvalenzbindungen  zwischen den Kettenmolekülen übertragen, was zu einer ungleichmäßigen Beanspruchung der Hauptvalenzen führt. Im Idealfall des kristallinen Grades  (s. Seite ) von 100 %, d. h. der ideal parallelen Lage der Ketten, ist ein rechnerischer Widerstand von 2000 N/mm gegen das Abgleiten der Ketten zu erwarten. Real ist bei Zellulose aber ein kristalliner Grad von 70 Prozent, damit liegt ein Zweiphasensystem  vor, welches maximal 800 N/mm erträgt [10].

Bei der Angabe der Dichte  ist zu beachten, daß diese durch wechselnde Luftfeuchte  (normal: = 65 %) oder durch nachfolgende Veredelung  der Faser noch ansteigen kann.